Contents

1 Introduction

The cow path problem is a classic in computer science and is fundamental to search theory. The problem, as formulated in one of the most celebrated papers that studies it (and the first, as far as I am aware, to actually call it “the cow path problem”) [25], is as follows: a cow named Bessie is standing at a crossroads with two paths leading off into unknown territory. On one of the paths lies a green pasture a distance $d\ge 1$ away while the other path simply goes on forever (see Figure 1). Bessie’s eyesight is very poor, so she can only tell whether she has reached the pasture or not when she is standing on it. What strategy should Bessie use to reach the pasture as quickly as possible?

Clearly, if Bessie knows which direction the pasture is, she can simply walk to it, traveling a total distance of $d$. We are interested in the case where Bessie does not know which direction the pasture is. Our goal is to find a strategy with the minimum competitive ratio, which is the ratio of the total distance Bessie walks using the strategy to the distance $d$ to the pasture. For a strategy $\mathcal{𝒜}$ let $T_{\mathcal{𝒜}}$ denote the total distance Bessie walks using the strategy. Then the competitive ratio of $\mathcal{𝒜}$ is $T_{\mathcal{𝒜}}∕d$. In other words, the competitive ratio tells us how many times further Bessie walks than she needs to in order to reach the pasture.

Motivation

Why study the cow path problem? The cow path problem is a classic problem in search theory and is the gateway to all kinds of even more interesting problems in search theory. Direct applications of the cow path problem include robotics applications (e.g., search and rescue missions) and hybrid algorithm execution (e.g., how long should we run an optimization algorithm before switching to a different one?).

The many variants of the cow path and related problems

A Quick Warm-Up

As a warm-up excersie, let’s consider the case where Bessie knows $d$ but not the direction of the pasture. In this case, there’s only one thing for her to do: pick a direction and walk along it a distance of $d$. If she travels a distance of $d$ and has not reached the pasture, then she knows the pasture is in the other direction.

There are two cases to consider:

1.

The pasture is in the direction Bessie walks first.

2.

The pasture is in the other direction.

In the first case, the competitive ratio is trivially $1$ – Bessie walks a distance of $d$ and reaches the pasture, travelling the best possible distance $d$ ($d∕d=1$). In the second case, however, Bessie walks a distance of $d$ in one direction, then has to walk back to the crossroads and walk a distance of $d$ in the other direction. In total, Bessie walks a distance of $3d$ to reach the pasture, so the competitive ratio is $3$.

That was easy! Now let’s consider the interesting case where Bessie does not know $d$ or the direction of the pasture.

2 An Optimal Strategy

Spoiler alert: it turns out that there is a relatively simple strategy that has a competitive ratio of just nine! In other words, this strategy guarantees that, no matter how far away the pasture is, Bessie will travel at most nine times the best possible distance to reach the pasture. The strategy is as follows:

1.

Bessie walks a distance of $1$ in one direction.

2.

If she has not reached the pasture, she walks back to the crossroads and walks a distance of $2$ in the other direction.

3.

If she has not reached the pasture, she walks back to the crossroads and walks a distance of $4$ in the first direction.

4.

She continues doing this, switching directions and doubling the distance she walks each time, until she reaches the pasture.

In other words, in each round (a trip out and back from the crossroads) $k=0,1,2,\dots <!--FUNCTION\; APPLICATION-->$, Bessie walks a distance of $2^k$ away from the crossroads and back in the opposite direction of the previous round.

Let’s start by analyzing the time it takes Bessie to reach the pasture using this strategy. First of all, observe that she’s guaranteed to reach it eventually since she’s increasing the distance she walks each round. Let $k$ denote the number of rounds it takes for Bessie to reach the pasture. Note that since $d\ge 1$, then $k>0$. We know two things about $d$ and $k$:

1.

$d\le 2^k$: Clearly, if Bessie reaches the pasture in round $k$, where she planned to walk a maximum distance of $2^k$, then the distance to the pasture must be at most $2^k$.

2.

$d>2^{k-2}$: In round $k-2$ Bessie walks a distance of $2^{k-2}$ in the same direction as in round $k$ (when she reaches the pasture). If $d\le 2^{k-2}$, then Bessie would have reached the pasture in round $k-2$ instead of round $k$.

We can write the total distance as a very simple geometric sum: $$\begin{array}{lll}\hfill 2\cdot 2^0+2\cdot 2^1+2\cdot 2^2+\dots <!--FUNCTION\; APPLICATION-->+2\cdot 2^{k-2}+2\cdot 2^{k-1}=2\sum _{i=0}^{k-1}{2}^i=2(2^k-1)=2^{k+1}-2& & \hfill \end{array}$$

The comeptitive ratio of the strategy is then:

$$\begin{array}{lll}\hfill \frac{2^{k+1}-2+d}{d}\le \frac{2^{k+1}}{d}+1& & \hfill \end{array}$$

We’re interested in the worst-case competitive ratio, so we want to maximize this expression with respect to $d$. As you can see, since $d$ is on the denominator, the competitive ratio is maximized when $d$ is minimized. Recall, however, that $2^{k-2}<d\le 2^k$, so the worst-case competitive ratio is given by:

$$\begin{array}{lll}\hfill \underset{d\to {(2^{k-2})}^{+}}{\lim <!--FUNCTION\; APPLICATION-->}[\frac{2^{k+1}}{d}+1]=\frac{2^{k+1}}{2^{k-2}}+1=2^3+1=9& & \hfill \end{array}$$

3 A Lower Bound

So we proved that the “doubling strategy” has a competitive ratio of $9$, but is this the best we can do? Why not triple in each round? or just increase our search distance by $50\%$?

In general, a geometrically increasing strategy follows the same pattern as the doubling strategy, but instead of doubling the distance Bessie walks each round, she walks a distance of $a^i$ in round $i=0,1,2,\dots <!--FUNCTION\; APPLICATION-->$. The doubling strategy is a special case of this where $a=2$. Could it be that a different value of $a$ could yield a better competitive ratio?

To answer this question, let’s analyze the competitive ratio of a general geometrically increasing strategy. Again, let $k$ denote the number of rounds it takes for Bessie to reach the pasture. Then we know that $d\le a^k$ and $d>a^{k-2}$. The total distance Bessie travels in the first $k-1$ rounds is:

$$\begin{array}{lll}\hfill 2\cdot a^0+2\cdot a^1+2\cdot a^2+\dots <!--FUNCTION\; APPLICATION-->+2\cdot a^{k-2}+2\cdot a^{k-1}=a\sum _{i=0}^{k-1}{a}^i=2(\frac{a^k-1}{a-1})& & \hfill \end{array}$$

The competitive ratio of the strategy is then:

$$\begin{array}{lll}\hfill \frac{2(\frac{a^k-1}{a-1})+d}{d}=\frac{2(\frac{a^k-1}{a-1})}{d}+1& & \hfill \end{array}$$

Again, observe that the competitive ratio is maximized when $d$ is minimized. Since $a^{k-2}<d\le a^k$, the worst-case competitive ratio is:

$$\begin{array}{lll}\hfill \frac{2(a^2-a^{2-k})}{a-1}+1& & \hfill \end{array}$$

Again, we’re interested in the worst-case competitive ratio, so we want to maximize this expression with respect to $k$. The competitive ratio is maximized when $k=2$, so the worst-case competitive ratio is:

$$\begin{array}{lll}\hfill \underset{k\to \infty }{\lim <!--FUNCTION\; APPLICATION-->}[\frac{2(a^2-a^{2-k})}{a-1}+1]=\frac{2(a^2-0)}{a-1}+1=\frac{2a^2}{a-1}+1& & \hfill \end{array}$$

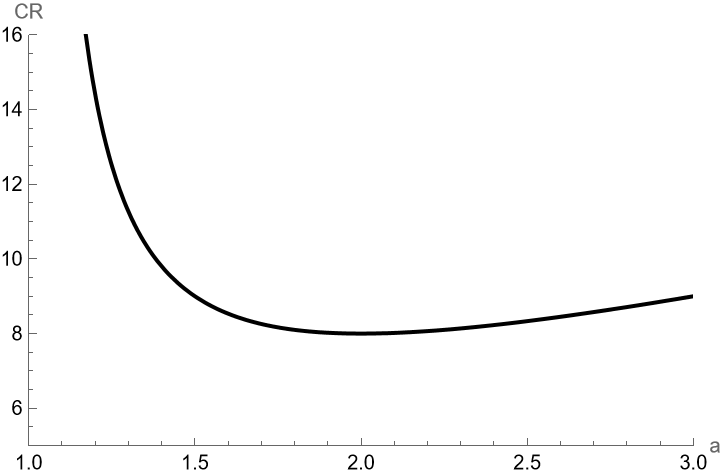
Great! We now have a general formula for the competitive ratio of any geometrically increasing strategy! Now the question is – what value of $a$ minimizes this expression? We’ll leave it as an excersise for the reader to show that the competitive ratio is minimized when $a=2$ (it’s not too difficult with a little calculus). Figure 2 show a plot, though, of the competitive ratio as a function of $a$. You can see very clearly that the best geometrically increasing strategy is the doubling strategy!

It’s important to note that we have only shown that the doubling strategy is the best geometrically increasing strategy. In order to prove a true lower bound for the problem, we would need to consider all possible strategies. In other words, we would need to show that there must exist a geometrically increasing strategy that does at least as well as any other strategy. This has indeed been proven, but it’s a bit more involved and I won’t go into it here. If interested, the following references all provide different complete proofs for the problem [2, 3, 11, 25].

4 Related Work and Further Reading

This problem was first studied by Bellman and Beck in the 1960’s [2, 3] (though with a different formulation) and has since been the subject of much research. As a fundamental problem in search theory, many variants of the original cow-path problem have been proposed and solved for different models and using a variety of techniques. For multi-agent systems, it is sometimes framed as an evacuation problem, where the goal is to minimize the time for every agent to find and travel to an exit whose location is unknown [4, 19]. The Group Search problem, on the other hand, requires any one agent to find the target [17]. These problems have been studied for many different topologies including the bounded line [5], the ring [24, 27], the disk [18], simple polygons [26], for multiple paths (the original problem is a two-path system - left and right from the starting location of the agent) [25], the plane [22], in graphs [4], and in trees [21]. Competitive algorithms for multi-agent systems have been proposed [4, 9, 18, 19, 20, 22, 24, 27], sometimes the agents to be faulty [20, 24] or mobile [14, 15]. A randomized algorithm has also been shown to dramatically improve the competitive ratio by a factor of almost $2$ for the original problem (and to a lesser extent for the multi-path variant) [25]. Search for mobile targets has also been studied [7, 11, 23].

Another related area of particular interest to me is delivery, whereby an agent or team of agents must cooperate to trasport a target object to a given location. Recently, there has been work in data delivery by systems of mobile agents on the line [8, 13], in the plane [10, 12, 16], and in graphs by energy-constrained agents [1, 6]. In 2021, we proposed the Pony Express Communication Problem [13], where agents must cooperate to transmit an object from one endpoint of a line segment to the other, is most similar to the problem we study in this paper. In the offline setting, where the locations of the object and all agents are known to every agent ahead of time, our problem is equivalent to the Pony Express Communication Problem, for which an optimal offline algorithm exists.

4.1 Our Work

[10]

Jared Coleman et al. “Delivery to Safety with Two Cooperating Robots”. In: CoRR abs/2210.04080 (2022). doi: 10.48550/arXiv.2210.04080. arXiv: 2210.04080.

[11]

Jared Coleman et al. “Line Search for an Oblivious Moving Target”. In: CoRR abs/2211.03686 (2022). doi: 10.48550/arXiv.2211.03686. arXiv: 2211.03686.

[12]

Jared Coleman et al. “Message Delivery in the Plane by Robots with Different Speeds”. In: Stabilization, Safety, and Security of Distributed Systems - 23rd International Symposium, SSS 2021, Virtual Event, November 17-20, 2021, Proceedings. Ed. by Colette Johnen, Elad Michael Schiller, and Stefan Schmid. Vol. 13046. Lecture Notes in Computer Science. Springer, 2021, pp. 305–319. doi: 10.1007/978-3- 030-91081-5\_20.

[13]

Jared Coleman et al. “The Pony Express Communication Problem”. In: Combinatorial Algorithms - 32nd International Workshop, IWOCA 2021, Ottawa, ON, Canada, July 5-7, 2021, Proceedings. Ed. by Paola Flocchini and Lucia Moura. Vol. 12757. Lecture Notes in Computer Science. Springer, 2021, pp. 208–222. doi: 10.1007/978-3-030-79987-8\_15.

[14]

Jared Ray Coleman, Lorand Cheng, and Bhaskar Krishnamachari. “Search and Rescue on the Line”. In: Structural Information and Communication Complexity - 30th International Colloquium, SIROCCO 2023, Alcalá de Henares, Spain, June 6-9, 2023, Proceedings. Ed. by Sergio Rajsbaum et al. Vol. 13892. Lecture Notes in Computer Science. Springer, 2023, pp. 297–316. doi: 10.1007/978- 3-031-32733-9\_13. url: https://doi.org/10.1007/978-3-031-32733-9%5C_13.

[15]

Jared Ray Coleman et al. “Linear Search for an Escaping Target with Unknown Speed”. In: Combinatorial Algorithms - 35th International Workshop, IWOCA 2024, Ischia, Italy, July 1-3, 2024, Proceedings. Ed. by Adele Anna Rescigno and Ugo Vaccaro. Vol. 14764. Lecture Notes in Computer Science. Springer, 2024, pp. 396–407. doi: 10.1007/978-3-031-63021-7\_30. url: https://doi.org/10.1007/978-3-031-63021-7%5C_30.

[16]

Jared Ray Coleman et al. “Optimal Delivery with a Faulty Drone”. In: CoRR abs/2404.17711 (2024). doi: 10 . 48550 / ARXIV . 2404 . 17711. arXiv: 2404 . 17711. url: https://doi.org/10.48550/arXiv.2404.17711.

References

[1]

Andreas Bärtschi and Thomas Tschager. “Energy-Efficient Fast Delivery by Mobile Agents”. In: Fundamentals of Computation Theory - 21st International Symposium, FCT 2017, Bordeaux, France, September 11-13, 2017, Proceedings. Ed. by Ralf Klasing and Marc Zeitoun. Vol. 10472. Lecture Notes in Computer Science. Springer, 2017, pp. 82–95. doi: 10.1007/978-3-662-55751-8\_8.

[2]

Anatole Beck. “On the linear search problem”. In: Israel Journal of Mathematics 2.4 (1964), pp. 221–228.

[3]

R. Bellman. “An optimal search”. In: Siam Review 5.3 (1963), pp. 274–274.

[4]

Piotr Borowiecki et al. “Distributed Evacuation in Graphs with Multiple Exits”. In: Structural Information and Communication Complexity - 23rd International Colloquium, SIROCCO 2016, Helsinki, Finland, July 19-21, 2016, Revised Selected Papers. Ed. by Jukka Suomela. Vol. 9988. Lecture Notes in Computer Science. 2016, pp. 228–241. doi: 10.1007/978-3-319-48314-6\_15.

[5]

Prosenjit Bose, Jean-Lou De Carufel, and Stephane Durocher. “Revisiting the Problem of Searching on a Line”. In: Algorithms - ESA 2013 - 21st Annual European Symposium, Sophia Antipolis, France, September 2-4, 2013. Proceedings. Ed. by Hans L. Bodlaender and Giuseppe F. Italiano. Vol. 8125. Lecture Notes in Computer Science. Springer, 2013, pp. 205–216. doi: 10.1007/978-3-642-40450- 4\_18.

[6]

Iago A. Carvalho, Thomas Erlebach, and Kleitos Papadopoulos. “On the fast delivery problem with one or two packages”. In: J. Comput. Syst. Sci. 115 (2021), pp. 246–263. doi: 10.1016/j.jcss.2020. 09.002.

[7]

Eowyn Cenek. “Chases and escapes by Paul J. Nahin”. In: SIGACT News 40.3 (2009), pp. 48–50. doi: 10.1145/1620491.1620500.

[8]

Jérémie Chalopin et al. “Data Delivery by Energy-Constrained Mobile Agents on a Line”. In: Automata, Languages, and Programming - 41st International Colloquium, ICALP 2014, Copenhagen, Denmark, July 8-11, 2014, Proceedings, Part II. Ed. by Javier Esparza et al. Vol. 8573. Lecture Notes in Computer Science. Springer, 2014, pp. 423–434. doi: 10.1007/978-3-662-43951-7\_36.

[9]

Marek Chrobak et al. “Group Search on the Line”. In: SOFSEM 2015: Theory and Practice of Computer Science - 41st International Conference on Current Trends in Theory and Practice of Computer Science, Pec pod Sněžkou, Czech Republic, January 24-29, 2015. Proceedings. Ed. by Giuseppe F. Italiano et al. Vol. 8939. Lecture Notes in Computer Science. Springer, 2015, pp. 164–176. doi: 10.1007/978-3-662-46078-8\_14.

[10]

Jared Coleman et al. “Delivery to Safety with Two Cooperating Robots”. In: CoRR abs/2210.04080 (2022). doi: 10.48550/arXiv.2210.04080. arXiv: 2210.04080.

[11]

Jared Coleman et al. “Line Search for an Oblivious Moving Target”. In: CoRR abs/2211.03686 (2022). doi: 10.48550/arXiv.2211.03686. arXiv: 2211.03686.

[12]

Jared Coleman et al. “Message Delivery in the Plane by Robots with Different Speeds”. In: Stabilization, Safety, and Security of Distributed Systems - 23rd International Symposium, SSS 2021, Virtual Event, November 17-20, 2021, Proceedings. Ed. by Colette Johnen, Elad Michael Schiller, and Stefan Schmid. Vol. 13046. Lecture Notes in Computer Science. Springer, 2021, pp. 305–319. doi: 10.1007/978-3- 030-91081-5\_20.

[13]

Jared Coleman et al. “The Pony Express Communication Problem”. In: Combinatorial Algorithms - 32nd International Workshop, IWOCA 2021, Ottawa, ON, Canada, July 5-7, 2021, Proceedings. Ed. by Paola Flocchini and Lucia Moura. Vol. 12757. Lecture Notes in Computer Science. Springer, 2021, pp. 208–222. doi: 10.1007/978-3-030-79987-8\_15.

[14]

Jared Ray Coleman, Lorand Cheng, and Bhaskar Krishnamachari. “Search and Rescue on the Line”. In: Structural Information and Communication Complexity - 30th International Colloquium, SIROCCO 2023, Alcalá de Henares, Spain, June 6-9, 2023, Proceedings. Ed. by Sergio Rajsbaum et al. Vol. 13892. Lecture Notes in Computer Science. Springer, 2023, pp. 297–316. doi: 10.1007/978- 3-031-32733-9\_13. url: https://doi.org/10.1007/978-3-031-32733-9%5C_13.

[15]

Jared Ray Coleman et al. “Linear Search for an Escaping Target with Unknown Speed”. In: Combinatorial Algorithms - 35th International Workshop, IWOCA 2024, Ischia, Italy, July 1-3, 2024, Proceedings. Ed. by Adele Anna Rescigno and Ugo Vaccaro. Vol. 14764. Lecture Notes in Computer Science. Springer, 2024, pp. 396–407. doi: 10.1007/978-3-031-63021-7\_30. url: https://doi.org/10.1007/978-3-031-63021-7%5C_30.

[16]

Jared Ray Coleman et al. “Optimal Delivery with a Faulty Drone”. In: CoRR abs/2404.17711 (2024). doi: 10 . 48550 / ARXIV . 2404 . 17711. arXiv: 2404 . 17711. url: https://doi.org/10.48550/arXiv.2404.17711.

[17]

Jurek Czyzowicz, Kostantinos Georgiou, and Evangelos Kranakis. “Group Search and Evacuation”. In: Distributed Computing by Mobile Entities, Current Research in Moving and Computing. Ed. by Paola Flocchini, Giuseppe Prencipe, and Nicola Santoro. Vol. 11340. Lecture Notes in Computer Science. Springer, 2019, pp. 335–370. doi: 10.1007/978-3-030-11072-7\_14.

[18]

Jurek Czyzowicz et al. “Evacuating Robots from a Disk Using Face-to-Face Communication”. In: Discret. Math. Theor. Comput. Sci. 22.4 (2020).

[19]

Jurek Czyzowicz et al. “Group Evacuation on a Line by Agents with Different Communication Abilities”. In: LIPIcs 212 (2021). Ed. by Hee-Kap Ahn and Kunihiko Sadakane, 57:1–57:24. doi: 10.4230/LIPIcs.ISAAC.2021.57.

[20]

Jurek Czyzowicz et al. “Search on a line with faulty robots”. In: Distributed Comput. 32.6 (2019), pp. 493–504. doi: 10.1007/s00446-017-0296-0.

[21]

Henri Devillez et al. “Two-Agent Tree Evacuation”. In: Structural Information and Communication Complexity - 28th International Colloquium, SIROCCO 2021, Wrocław, Poland, June 28 - July 1, 2021, Proceedings. Ed. by Tomasz Jurdzinski and Stefan Schmid. Vol. 12810. Lecture Notes in Computer Science. Springer, 2021, pp. 204–221. doi: 10.1007/978-3-030-79527-6\_12.

[22]

Ofer Feinerman et al. “Collaborative search on the plane without communication”. In: ACM Symposium on Principles of Distributed Computing, PODC ’12, Funchal, Madeira, Portugal, July 16-18, 2012. Ed. by Darek Kowalski and Alessandro Panconesi. ACM, 2012, pp. 77–86. doi: 10.1145/2332432. 2332444.

[23]

Shmuel Gal. “Search games”. In: Wiley encyclopedia of operations research and management science (2010).

[24]

Konstantinos Georgiou et al. “Optimal Circle Search Despite the Presence of Faulty Robots”. In: Algorithms for Sensor Systems - 15th International Symposium on Algorithms and Experiments for Wireless Sensor Networks, ALGOSENSORS 2019, Munich, Germany, September 12-13, 2019, Revised Selected Papers. Ed. by Falko Dressler and Christian Scheideler. Vol. 11931. Lecture Notes in Computer Science. Springer, 2019, pp. 192–205. doi: 10.1007/978-3-030-34405-4\_11.

[25]

Ming-Yang Kao, John H. Reif, and Stephen R. Tate. “Searching in an Unknown Environment: An Optimal Randomized Algorithm for the Cow-Path Problem”. In: (1993). Ed. by Vijaya Ramachandran, pp. 441–447.

[26]

Jon M. Kleinberg. “On-line Search in a Simple Polygon”. In: Proceedings of the Fifth Annual ACM-SIAM Symposium on Discrete Algorithms. 23-25 January 1994, Arlington, Virginia, USA. Ed. by Daniel Dominic Sleator. ACM/SIAM, 1994, pp. 8–15.

[27]

Kevin Spieser and Emilio Frazzoli. “The Cow-Path Game: A competitive vehicle routing problem”. In: Proceedings of the 51th IEEE Conference on Decision and Control, CDC 2012, December 10-13, 2012, Maui, HI, USA. IEEE, 2012, pp. 6513–6520. doi: 10.1109/CDC.2012.6426279.