Contents

1 Introduction

Scheduling a task graph on networked computers is a fundamental problem in distributed computing. Essentially, the goal is to assign computational tasks to different compute nodes in such a way that minimizes/maximizes some performance metric (e.g., total execution time, energy consumption, throughput, etc.). We will focus on the task scheduling problem concerning heterogeneous task graphs and compute networks with the objective of minimizing makespan (total execution time) under the related machines model¹.

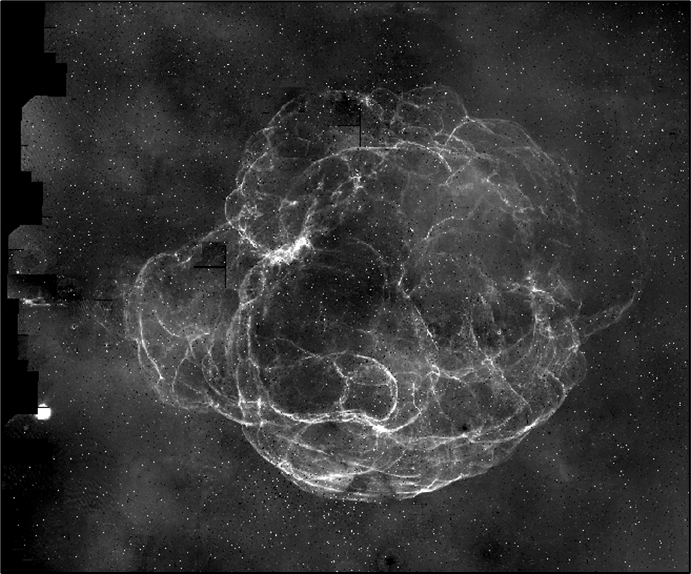
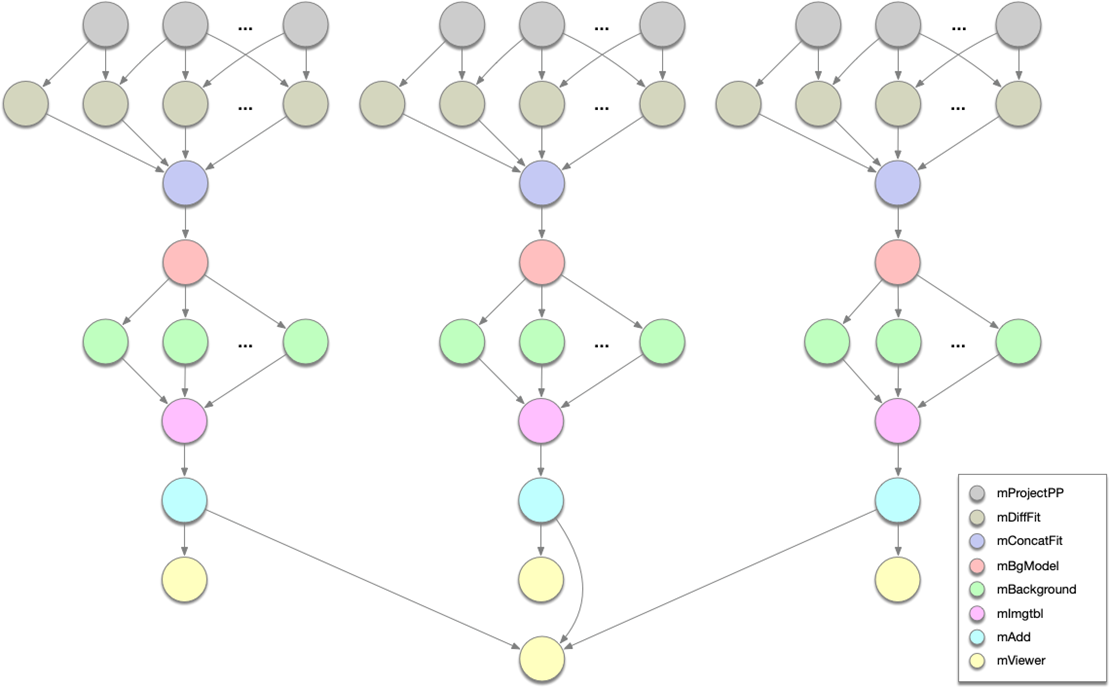
It is common to model distributed applications as task graphs, where nodes represent computational tasks and directed edges represent precedence constraints and the flow of input/output data. As a result, task scheduling pops up all over the place - from machine learning and scientific workflows, to IoT/edge computing applications, to data processing pipelines used all over industry. Figure 1 depicts a scientific workflow application used by Caltech astronomers to generate science-grade mosaics from astronomical imagery [57].

1.1 Problem Definition

Let us denote the task graph as $G=(T,D)$, where $T$ is the set of tasks and $D$ contains the directed edges or dependencies between these tasks. An edge $(t,t^{\prime })\in D$ implies that the output from task $t$ is required input for task $t^{\prime }$. Thus, task $t^{\prime }$ cannot start executing until it has received the output of task $t$. This is often referred to as a precedence constraint. For a given task $t\in T$, its compute cost is represented by $c(t)\in {ℝ}^{+}$ and the size of the data exchanged between two dependent tasks, $(t,t^{\prime })\in D$, is $c(t,t^{\prime })\in {ℝ}^{+}$. Let $N=(V,E)$ denote the compute node network, where $N$ is a complete undirected graph. $V$ is the set of nodes and $E$ is the set of edges. The compute speed of a node $v\in V$ is $s(v)\in {ℝ}^{+}$ and the communication strength between nodes $(v,v^{\prime })\in E$ is $s(v,v^{\prime })\in {ℝ}^{+}$. Under the related machines model [25], the execution time of a task $t\in T$ on a node $v\in V$ is $\frac{c(t)}{s(v)}$, and the data communication time between tasks $(t,t^{\prime })\in D$ from node $v$ to node $v^{\prime }$ (i.e., $t$ executes on $v$ and $t^{\prime }$ executes on $v^{\prime }$) is $\frac{c(t,t^{\prime })}{s(v,v^{\prime })}$.

The goal is to schedule the tasks on different compute nodes in such a way that minimizes the makespan (total execution time) of the task graph. Let $\mathcal{𝒜}$ denote a task scheduling algorithm. Given a problem instance $(N,G)$ which represents a network/task graph pair, let $S_{\mathcal{𝒜},N,G}$ denote the schedule produced by $\mathcal{𝒜}$ for $(N,G)$. A schedule is a mapping from each task to a triple $(v,r,e)$ where $v$ is the node on which the task is scheduled, $r$ is the start time, and $e$ is the end time. A valid schedule must satisfy the following properties

• All tasks must be scheduled: for all $t\in T$, $S_{\mathcal{𝒜},N,G}(t)=(v,r,e)$ must exist such that $v\in V$ and $0\le r\le e$.

• All tasks must have valid start and end times:

  $$\forall <!--FUNCTION\; APPLICATION-->t\in T,S_{\mathcal{𝒜},N,G}(t)=(v,r,e)\Rightarrow e-r=\frac{c(t)}{s(v)}$$

• Only one task can be scheduled on a node at a time (i.e., their start/end times cannot overlap):

  $$\forall <!--FUNCTION\; APPLICATION-->t,t^{\prime }\in T,t\ne t^{\prime },S_{\mathcal{𝒜},N,G}(t)=(v,r,e)\wedge S_{\mathcal{𝒜},N,G}(t^{\prime })=(v,r^{\prime },e^{\prime })\Rightarrow e\le r^{\prime }\vee e^{\prime }\le r$$

• A task cannot start executing until all of its dependencies have finished executing and their outputs have been received at the node on which the task is scheduled:

  $$\forall <!--FUNCTION\; APPLICATION-->(t,t^{\prime })\in D,S_{\mathcal{𝒜},N,G}(t)=(v,r,e)\wedge S_{\mathcal{𝒜},N,G}(t^{\prime })=(v^{\prime },r^{\prime },e^{\prime })\Rightarrow e+\frac{c(t,t^{\prime })}{s(v,v^{\prime })}\le r^{\prime }$$

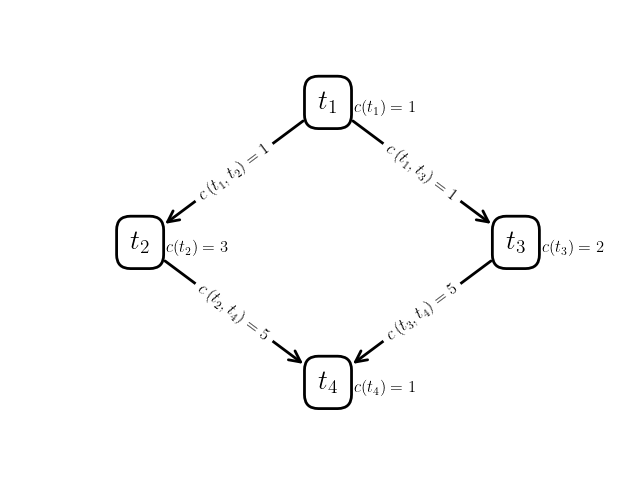
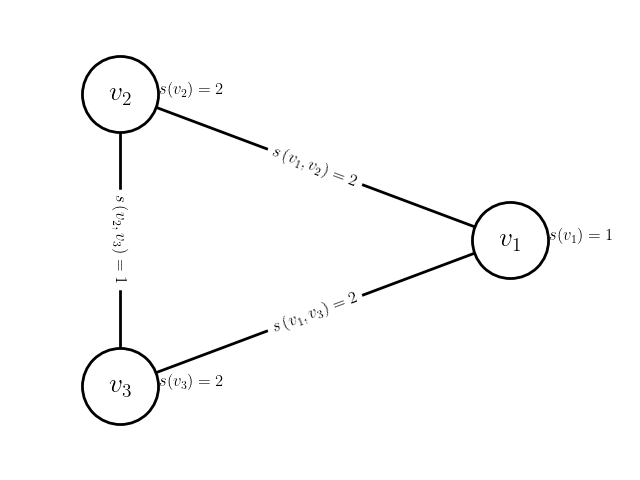
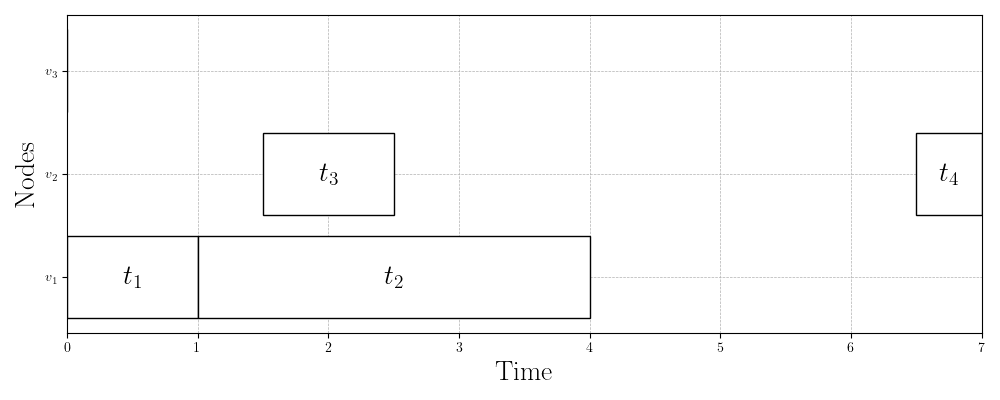
Figure 2 depicts an example problem instance (task graph and network) and solution (schedule). We define the makespan of the schedule $S_{\mathcal{𝒜},N,G}$ as the time at which the last task finishes executing:

1.2 Example 1

Take a look at the task graph, network, and schedule in Figure 2. Let us start by verifying that this is a valid schedule for the problem instance (network/task graph pair). First, task $t_1$ is scheduled to run on node $v_1$. Clearly this is valid, since $t_1$ has no dependencies. When $t_1$ finishes running at time $1$, which is valid since the cost of task $t_1$ is $1$ and the speed of node $v_1$ is $1$ ($1∕1=1$). Then, $t_2$ immediately starts running at time $1$ on node $v_1$. Again, this is clearly valid since there is no communication delay in sending the outputs from task $t_1$ to another node before running task $t_2$. Task $t_3$, on the other hand, is scheduled to run on node $v_2$. In this case, $1$ unit of output data from task $t_1$ must be sent to node $v_2$ as input data to task $t_3$. The communication link between nodes $v_1$ and $v_2$ is $2$, so this communication takes $1∕2$ units of time. Thus, the start time of task $t_3$ is valid since it is exactly $1∕2$ units of time after task $t_1$ terminates. It’s easy to verify that tasks $t_3$ and $t_2$ have valid runtimes according to their costs and the speeds of the nodes they’re running on. Finally, task $t_4$ is scheduled to run on node $v_2$. Before it can start running, though, the $5$ units of output data from task $t_2$ must be sent from node $v_1$ to node $v_2$ over a communication link of strength $2$. Thus, the start time of task $t_4$ is correct ($5∕2=2.5$ units of time after task $t_2$’s finish time). Thus, the schedule in Figure 2c is valid and has a makespan of $7$.

2 The HEFT Scheduling Algorithm

This task scheduling problem has long been known to be NP-Hard and was recently shown to also be not polynomial-time approximable within a constant factor [7]. As a result, many heuristic algorithms that aren’t guaranteed to produce an optimal schedule but that, in practice, have been shown to work reasonably well have been proposed over the past decades. One of the most commonly used of these algorithms is HEFT (Heterogeneous Earliest Finish Time) [69]. HEFT is a list-scheduling algorithm, which essentially means it first computes priorities for each of the tasks in the task graph and then schedules the tasks greedily in order of their priority on the “best” node (the one that minimizes the task’s finish time, given previously scheduled tasks). Here is a summary of the algorithm:

1.

calculate average compute times for each task: $$\overline{\mathtt{\text{comp}}}(t)=\frac{1}{\left|V\right|}\sum _{v\in V}\frac{c(t)}{s(v)}\forall <!--FUNCTION\; APPLICATION-->t\in T$$

2.

calculate average communication times for each dependency: $$\overline{\mathtt{\text{comm}}}(t_1,t_2)=\frac{1}{\left|E\right|}\sum _{(v_1,v_2)\in E,v_1\ne v_2}\frac{c(t_1,t_2)}{s(v_1,v_2)}\forall <!--FUNCTION\; APPLICATION-->(t_1,t_2)\in D$$

3.

calculate the upward rank of each task (recursively): $$\mathtt{\text{urank}}(t)=\overline{\mathtt{\text{comp}}}(t)+\underset{t^{\prime }\in T|(t,t^{\prime })\in D}{\max <!--FUNCTION\; APPLICATION-->}\left\{\overline{\mathtt{\text{comm}}}(t,t^{\prime })+\mathtt{\text{urank}}(t^{\prime })\right\}\forall <!--FUNCTION\; APPLICATION-->t\in T$$

4.

In descending order of task upward ranks, greedily schedule each task on the node that minimizes its earliest possible finish time given previously scheduled tasks.

The average compute costs, communication costs, and upward ranks for the problem instance in Figure 2 are presented in Tables 1, 2, and 3, respectively.

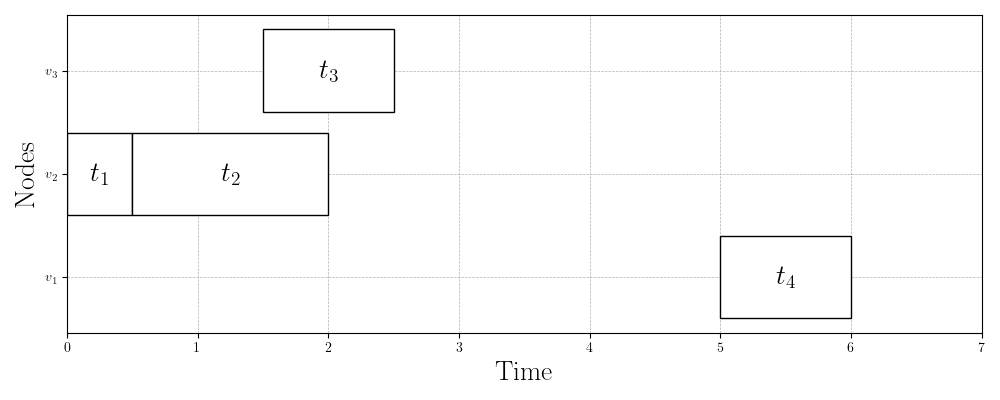
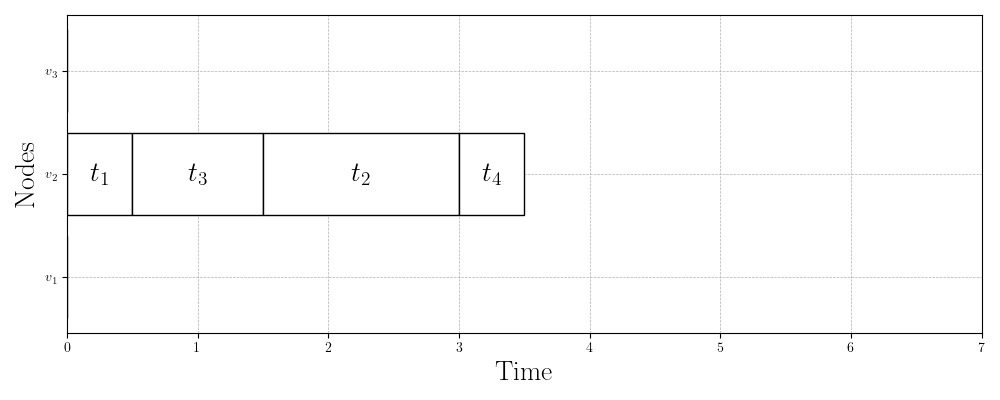
Figure 3 shows three valid schedules for the same problem instance. Figure 3a shows the first schedule we validated in the previous section with makespan $7$. Figure 3b shows the schedule that the HEFT algorithm produces with a slightly better makespan of $6$. Finally, Figure 3c shows the best schedule for this problem instance, which has a makespan of just $3.5$. This is almost half the makespan of the schedule that HEFT (one of the most widely used scheduling algorithms) produces!

Questions to Consider

1.

Upward rank has the important property that a task’s upward rank is always greater than the upward rank of its dependent tasks. Why is this important?

2.

What is the runtime of HEFT in terms of $\left|T\right|$, $\left|D\right|$, $\left|V\right|$, and $\left|E\right|$?

3.

Why does HEFT perform poorly on the problem instance in Figure 2? Can you think of an algorithm that would do better?

3 My Research Interests

Task scheduling is an fundamental problem in computer science that pops up everywhere. In this lecture, we formalized the task scheduling problem for heterogeneous task graphs and compute networks with the objective of minimizing makespan (total execution time) under the related machines model. Many other interesting variants of task scheduling problem exist (see [27]).

We also learned HEFT, one of the most popular task scheduling heuristic algorithms, and saw a problem instance on which it performs rather poorly. Hundreds of heuristic algorithms have been proposed in the literature over the past decades ([11] has nice descriptions of eleven scheduling algorithms). Due to their reliance on heuristics (since the problem is NP-Hard), all of these algorithms have problem instances on which they perform very poorly. The performance boundaries between heuristic algorithms are not well-understood, however. This is an area of my research. We look at methodologies for comparing task scheduling algorithms to better understand the conditions under which they perform well and poorly.

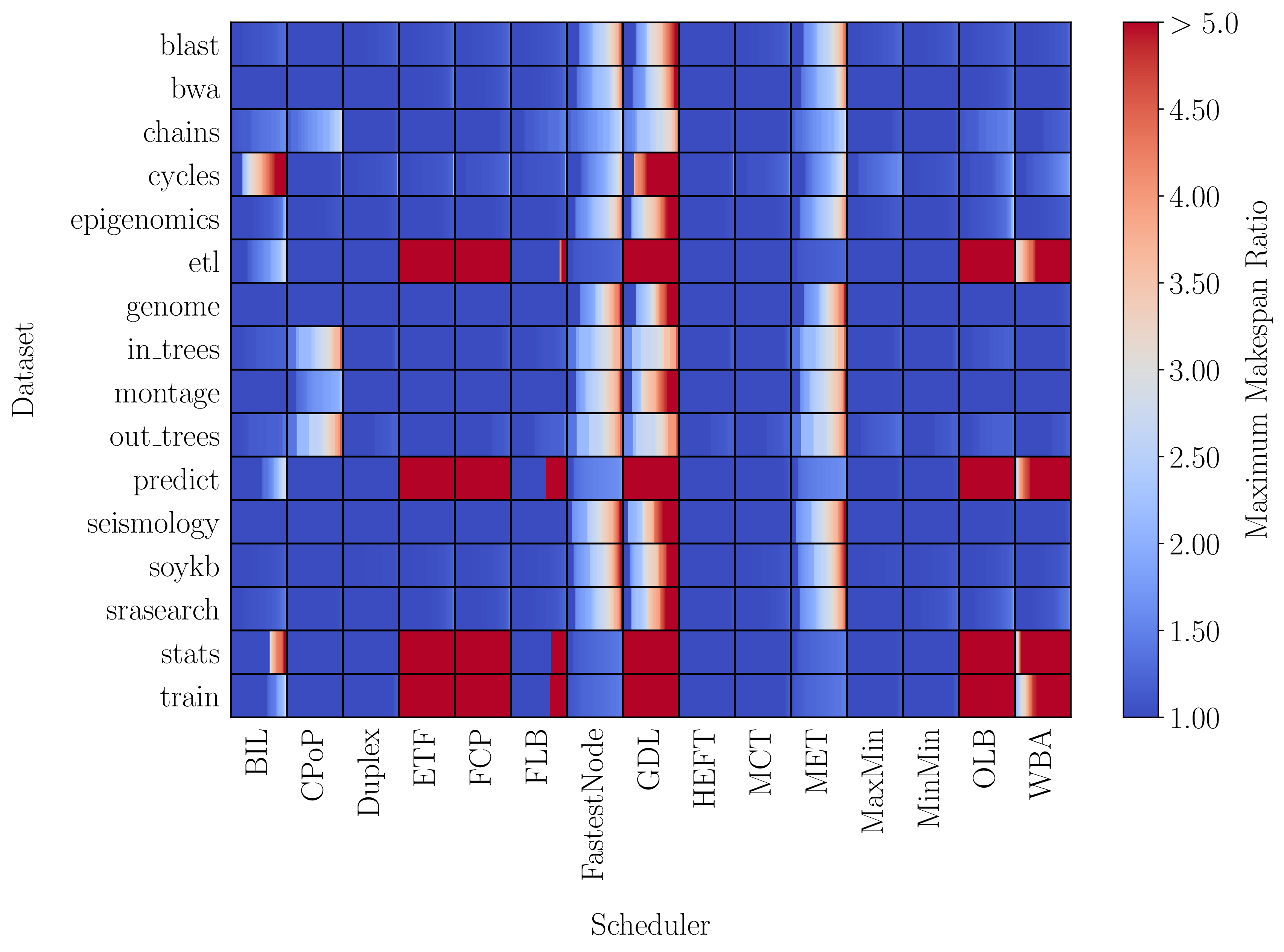
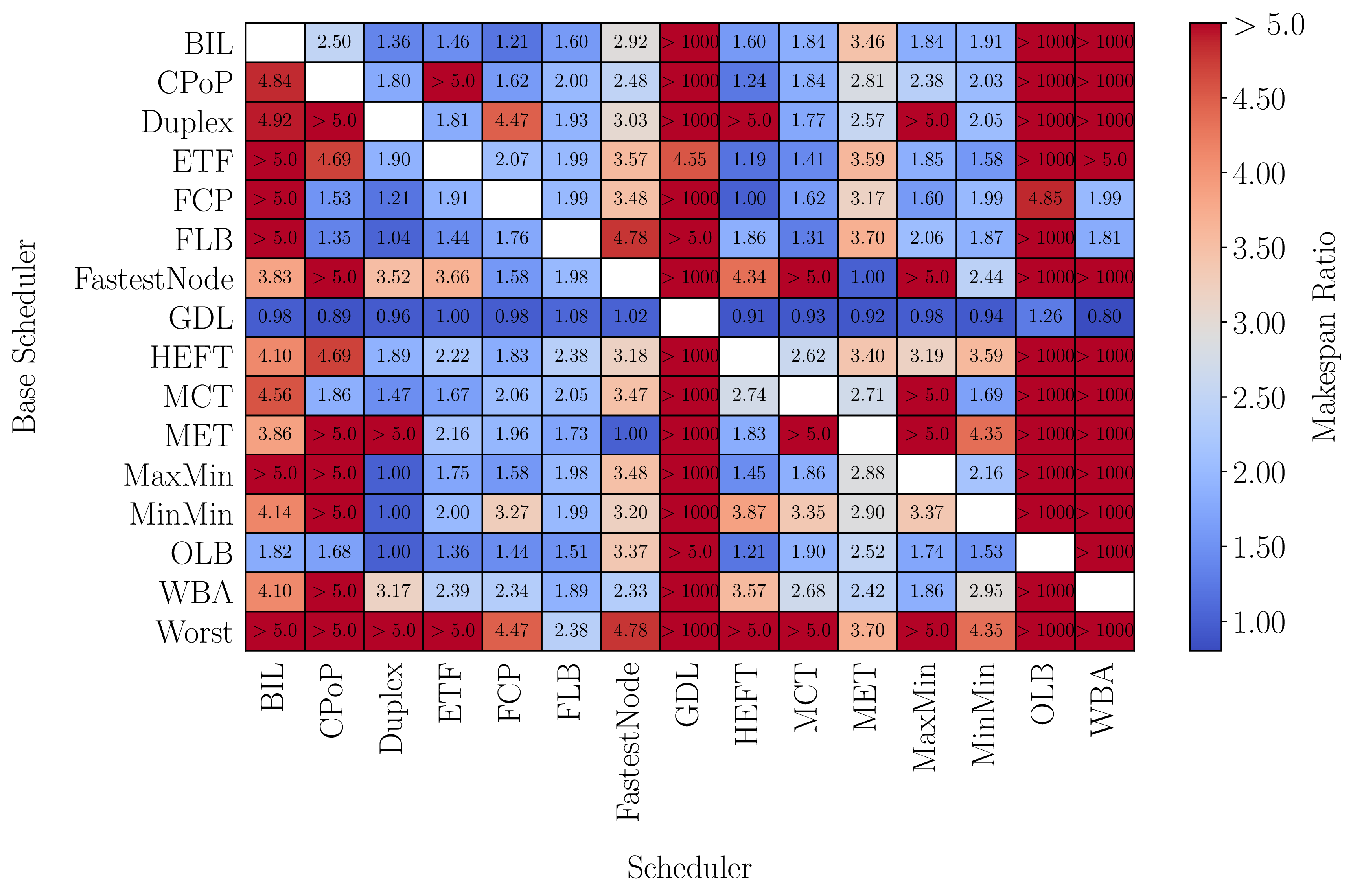
Figures 4 and 5 depict results from our efforts in this area. Figure 4 shows benchmarking results for 15 scheduling algorithms on 16 datasets. The color represents the maximum makespan ratio (MMR) of an algorithm on a problem instance in a given dataset. The MMR of an algorithm is essentially how many times worse the algorithm performs on a particular problem instance compared to the other scheduling algorithms. For example, on some problem instances in the cycles dataset, the BIL algorithm performs more than five times worse than another one of the 15 algorithms! On other problem instances in the same dataset, however, the algorithm performs well (MMR=1). Figure 5 shows results from our own comparison method that pits algorithms against each other and tries to find a problem instance where one algorithm maximally underperforms compared to another. Our hope is that by identifying these kinds of problem instances, we can better understand the conditions under which algorithms perform well/poorly.

4 Bibliography

The following bibliography is organized into different categories. Some papers apply to more than one category and therefore appear multiple times.

4.1 Our Work

[3]

Tzanis Anevlavis et al. “Network synthesis for tactical environments: scenario, challenges, and opportunities”. In: Artificial Intelligence and Machine Learning for Multi-Domain Operations Applications IV 12113 (2022). Publisher: SPIE, pp. 199–206. doi: https://doi.org/10.1117/12. 2619048.

[13]

Jared Coleman. SAGA: Scheduling Algorithms Gathered. Github. https://github.com/ANRGUSC/saga. 2023. url: https://github.com/ANRGUSC/saga.

[14]

Jared Coleman and Bhaskar Krishnamachari. Scheduling Algorithms Gathered: A Framework for Implementing, Evaluating, and Comparing Task Graph Scheduling Algorithms. Tech. rep. University of Southern California, 2023.

[15]

Jared Coleman et al. “Graph Convolutional Network-based Scheduler for Distributing Computation in the Internet of Robotic Things”. In: MILCOM 2022-2022 IEEE Military Communications Conference (MILCOM). IEEE, 2022, pp. 1070–1075. doi: 10.1109/MILCOM55135.2022.10017673.

[16]

Jared Coleman et al. “Multi-objective network synthesis for dispersed computing in tactical environments”. In: Signal Processing, Sensor/Information Fusion, and Target Recognition XXXI. Vol. 12122. SPIE, 2022, pp. 132–137. doi: https://doi.org/10.1117/12.2616187.

[17]

Jared Ray Coleman and Bhaskar Krishnamachari. “Comparing Task Graph Scheduling Algorithms: An Adversarial Approach”. In: CoRR abs/2403.07120 (2024). doi: 10.48550/ARXIV.2403.07120. arXiv: 2403.07120. url: https://doi.org/10.48550/arXiv.2403.07120.

[18]

Jared Ray Coleman et al. “Parameterized Task Graph Scheduling Algorithm for Comparing Algorithmic Components”. In: CoRR abs/2403.07112 (2024). doi: 10.48550/ARXIV.2403.07112. arXiv: 2403.07112. url: https://doi.org/10.48550/arXiv.2403.07112.

[21]

Daniel D’Souza et al. “Graph Convolutional Network-based Scheduler for Distributing Computation in the Internet of Robotic Things”. The 2nd Student Design Competition on Networked Computing on the Edge. url=https://github.com/ANRGUSC/gcnschedule-turtlenet. 2022.

4.2 Theory

[6]

Abbas Bazzi and Ashkan Norouzi-Fard. “Towards Tight Lower Bounds for Scheduling Problems”. In: Algorithms - ESA 2015 - 23rd Annual European Symposium, Patras, Greece, September 14-16, 2015, Proceedings. Ed. by Nikhil Bansal and Irene Finocchi. Vol. 9294. Lecture Notes in Computer Science. Springer, 2015, pp. 118–129. doi: 10 . 1007 / 978 - 3 - 662 - 48350 - 3 \ _11. url: https://doi.org/10.1007/978-3-662-48350-3%5C_11.

[25]

R. L. Graham. “Bounds on Multiprocessing Timing Anomalies”. In: SIAM Journal on Applied Mathematics 17.2 (1969), pp. 416–429. doi: 10.1137/0117039. eprint: https://doi.org/10.1137/0117039. url: https://doi.org/10.1137/0117039.

[26]

R. L. Graham. “Bounds on Multiprocessing Timing Anomalies”. In: SIAM Journal on Applied Mathematics 17.2 (1969), pp. 416–429. doi: 10.1137/0117039. eprint: https://doi.org/10.1137/0117039. url: https://doi.org/10.1137/0117039.

[27]

R.L. Graham et al. “Optimization and Approximation in Deterministic Sequencing and Scheduling: a Survey”. In: Discrete Optimization II. Ed. by P.L. Hammer, E.L. Johnson, and B.H. Korte. Vol. 5. Annals of Discrete Mathematics. Elsevier, 1979, pp. 287–326. doi: https://doi.org/10.1016/S0167-5060(08)70356-X. url: https://www.sciencedirect.com/science/article/pii/S016750600870356X.

[32]

Jing-Jang Hwang et al. “Scheduling Precedence Graphs in Systems with Interprocessor Communication Times”. In: SIAM J. Comput. 18.2 (1989), pp. 244–257. doi: 10.1137/0218016.

[33]

Jing-Jang Hwang et al. “Scheduling Precedence Graphs in Systems with Interprocessor Communication Times”. In: SIAM J. Comput. 18.2 (1989), pp. 244–257. doi: 10 . 1137 / 0218016. url: https://doi.org/10.1137/0218016.

[65]

Oliver Sinnen. Task Scheduling for Parallel Systems. Wiley series on parallel and distributed computing. Wiley, 2007. isbn: 978-0-471-73576-2. url: http://eu.wiley.com/WileyCDA/WileyTitle/productCd-0471735760.html.

4.3 Scheduling Algorithms

[4]

R. Armstrong, D. Hensgen, and T. Kidd. “The relative performance of various mapping algorithms is independent of sizable variances in run-time predictions”. In: Proceedings Seventh Heterogeneous Computing Workshop (HCW’98). 1998, pp. 79–87. doi: 10.1109/HCW.1998.666547.

[5]

Yossi Azar and Amir Epstein. “Convex programming for scheduling unrelated parallel machines”. In: Proceedings of the thirty-seventh annual ACM symposium on Theory of computing. 2005, pp. 331–337.

[9]

James Blythe et al. “Task scheduling strategies for workflow-based applications in grids”. In: 5th International Symposium on Cluster Computing and the Grid (CCGrid 2005), 9-12 May, 2005, Cardiff, UK. IEEE Computer Society, 2005, pp. 759–767. doi: 10.1109/CCGRID.2005.1558639. url: https://doi.org/10.1109/CCGRID.2005.1558639.

[11]

Tracy D. Braun et al. “A Comparison of Eleven Static Heuristics for Mapping a Class of Independent Tasks onto Heterogeneous Distributed Computing Systems”. In: J. Parallel Distributed Comput. 61.6 (2001), pp. 810–837. doi: 10 . 1006 / jpdc . 2000 . 1714. url: https://doi.org/10.1006/jpdc.2000.1714.

[28]

Mohammed Zaki Hasan and Hussain Al-Rizzo. “Task scheduling in Internet of Things cloud environment using a robust particle swarm optimization”. In: Concurrency and Computation: Practice and Experience 32.2 (2020), e5442.

[31]

Diyi Hu and Bhaskar Krishnamachari. “Throughput Optimized Scheduler for Dispersed Computing Systems”. In: 7th IEEE International Conference on Mobile Cloud Computing, Services, and Engineering, MobileCloud 2019, Newark, CA, USA, April 4-9, 2019. IEEE, 2019, pp. 76–84. doi: 10.1109/MOBILECLOUD.2019.00018. url: https://doi.org/10.1109/MobileCloud.2019.00018.

[32]

Jing-Jang Hwang et al. “Scheduling Precedence Graphs in Systems with Interprocessor Communication Times”. In: SIAM J. Comput. 18.2 (1989), pp. 244–257. doi: 10.1137/0218016.

[34]

Michael A. Iverson and Füsun Özgüner. “Hierarchical, competitive scheduling of multiple DAGs in a dynamic heterogeneous environment”. In: Distributed Syst. Eng. 6 (1999), pp. 112–.

[42]

Mohit Kumar and Subhash Chander Sharma. “Dynamic load balancing algorithm for balancing the workload among virtual machine in cloud computing”. In: Procedia computer science 115 (2017), pp. 322–329.

[44]

Chung-Yee Lee et al. “Multiprocessor scheduling with interprocessor communication delays”. In: Operations Research Letters 7.3 (1988), pp. 141–147. issn: 0167-6377. doi: https://doi.org/10.1016/0167-6377(88)90080-6. url: https://www.sciencedirect.com/science/article/pii/0167637788900806.

[45]

Shengzhong Liu et al. “Real-time task scheduling for machine perception in in intelligent cyber-physical systems”. In: IEEE Transactions on Computers (2021).

[49]

Rodrigo Fernandes de Mello et al. “Grid job scheduling using Route with Genetic Algorithm support”. In: Telecommunication Systems 38 (2008), pp. 147–160.

[50]

Tchimou N’Takpé and Frédéric Suter. “Critical Path and Area Based Scheduling of Parallel Task Graphs on Heterogeneous Platforms”. In: 12th International Conference on Parallel and Distributed Systems, ICPADS 2006, Minneapolis, Minnesota, USA, July 12-15, 2006. IEEE Computer Society, 2006, pp. 3–10. doi: 10.1109/ICPADS.2006.32. url: https://doi.org/10.1109/ICPADS.2006.32.

[52]

Hyunok Oh and Soonhoi Ha. “A Static Scheduling Heuristic for Heterogeneous Processors”. In: Euro-Par ’96 Parallel Processing, Second International Euro-Par Conference, Lyon, France, August 26-29, 1996, Proceedings, Volume II. Ed. by Luc Bougé et al. Vol. 1124. Lecture Notes in Computer Science. Springer, 1996, pp. 573–577. doi: 10 . 1007 / BFb0024750. url: https://doi.org/10.1007/BFb0024750.

[53]

A. Poylisher et al. “Tactical Jupiter: Dynamic Scheduling of Dispersed Computations in Tactical MANETs”. In: MILCOM 2021 - 2021 IEEE Military Communications Conference (MILCOM). 2021, pp. 102–107. doi: 10.1109/MILCOM52596.2021.9652937.

[54]

Andrei Radulescu and Arjan J. C. van Gemund. “Fast and Effective Task Scheduling in Heterogeneous Systems”. In: 9th Heterogeneous Computing Workshop, HCW 2000, Cancun, Mexico, May 1, 2000. IEEE Computer Society, 2000, pp. 229–238. doi: 10 . 1109 / HCW . 2000 . 843747. url: https://doi.org/10.1109/HCW.2000.843747.

[55]

Hesham El-Rewini and T. G. Lewis. “Scheduling parallel program tasks onto arbitrary target machines”. In: Journal of Parallel and Distributed Computing 9.2 (1990), pp. 138–153. issn: 0743-7315. doi: https : / / doi . org / 10 . 1016 / 0743 - 7315(90 ) 90042 - N. url: https://www.sciencedirect.com/science/article/pii/074373159090042N.

[59]

Henrique Yoshikazu Shishido et al. “Genetic-based algorithms applied to a workflow scheduling algorithm with security and deadline constraints in clouds”. In: Computers & Electrical Engineering 69 (2018), pp. 378–394.

[61]

Gilbert C. Sih and Edward A. Lee. “A Compile-Time Scheduling Heuristic for Interconnection-Constrained Heterogeneous Processor Architectures”. In: IEEE Trans. Parallel Distributed Syst. 4.2 (1993), pp. 175–187. doi: 10.1109/71.207593. url: https://doi.org/10.1109/71.207593.

[66]

Rajesh Sudarsan and Calvin J Ribbens. “Combining performance and priority for scheduling resizable parallel applications”. In: Journal of Parallel and Distributed Computing 87 (2016), pp. 55–66.

[69]

Haluk Topcuoglu, Salim Hariri, and Min-You Wu. “Task Scheduling Algorithms for Heterogeneous Processors”. In: 8th Heterogeneous Computing Workshop, HCW 1999, San Juan, Puerto Rico, April12, 1999. IEEE Computer Society, 1999, pp. 3–14. doi: 10.1109/HCW.1999.765092. url: https://doi.org/10.1109/HCW.1999.765092.

[72]

Ondrej Votava, Peter Macejko, and Jan Janecek. “Dynamic Local Scheduling of Multiple DAGs in Distributed Heterogeneous Systems”. In: DATESO. 2015.

4.4 Surveys and Algorithm Comparsison Papers

[2]

Mohammad Reza Alizadeh et al. “Task scheduling approaches in fog computing: A systematic review”. In: International Journal of Communication Systems 33.16 (2020), e4583.

[8]

Jakub Beránek, Stanislav Böhm, and Vojtech Cima. “Analysis of workflow schedulers in simulated distributed environments”. In: J. Supercomput. 78.13 (2022), pp. 15154–15180. doi: 10.1007/s11227- 022-04438-y. url: https://doi.org/10.1007/s11227-022-04438-y.

[10]

T.D. Braun et al. “A comparison study of static mapping heuristics for a class of meta-tasks on heterogeneous computing systems”. In: Proceedings. Eighth Heterogeneous Computing Workshop (HCW’99). 1999, pp. 15–29. doi: 10.1109/HCW.1999.765093.

[12]

Louis-Claude Canon et al. “Comparative Evaluation Of The Robustness Of DAG Scheduling Heuristics”. In: Grid Computing - Achievements and Prospects: CoreGRID Integration Workshop 2008, Hersonissos, Crete, Greece, April 2-4, 2008. Ed. by Sergei Gorlatch, Paraskevi Fragopoulou, and Thierry Priol. Springer, 2008, pp. 73–84. doi: 10.1007/978-0-387-09457-1\_7. url: https://doi.org/10.1007/978-0-387-09457-1%5C_7.

[27]

R.L. Graham et al. “Optimization and Approximation in Deterministic Sequencing and Scheduling: a Survey”. In: Discrete Optimization II. Ed. by P.L. Hammer, E.L. Johnson, and B.H. Korte. Vol. 5. Annals of Discrete Mathematics. Elsevier, 1979, pp. 287–326. doi: https://doi.org/10.1016/S0167-5060(08)70356-X. url: https://www.sciencedirect.com/science/article/pii/S016750600870356X.

[30]

Essam H. Houssein et al. “Task Scheduling in Cloud Computing based on Meta-heuristics: Review, Taxonomy, Open Challenges, and Future Trends”. In: Swarm Evol. Comput. 62 (2021), p. 100841. doi: 10.1016/j.swevo.2021.100841. url: https://doi.org/10.1016/j.swevo.2021.100841.

[43]

Y.-K. Kwok and I. Ahmad. “Benchmarking the task graph scheduling algorithms”. In: Proceedings of the First Merged International Parallel Processing Symposium and Symposium on Parallel and Distributed Processing. 1998, pp. 531–537. doi: 10.1109/IPPS.1998.669967.

[48]

Ashish Kumar Maurya and Anil Kumar Tripathi. “On benchmarking task scheduling algorithms for heterogeneous computing systems”. In: J. Supercomput. 74.7 (2018), pp. 3039–3070. doi: 10.1007/ S11227-018-2355-0. url: https://doi.org/10.1007/s11227-018-2355-0.

[51]

Pooria Namyar et al. “Minding the gap between Fast Heuristics and their Optimal Counterparts”. In: Hot Topics in Networking. acm. Nov. 2022. url: https://www.microsoft.com/en-us/research/publication/minding-the-gap-between-fast-heuristics-and-their-optimal-counterparts/.

[64]

Khushboo Singh, Mahfooz Alam, and Sushil Kumar Sharma. “A survey of static scheduling algorithm for distributed computing system”. In: International Journal of Computer Applications 129.2 (2015), pp. 25–30. doi: 10.5120/ijca2015906828.

[73]

Huijun Wang and Oliver Sinnen. “List-Scheduling versus Cluster-Scheduling”. In: IEEE Trans. Parallel Distributed Syst. 29.8 (2018), pp. 1736–1749. doi: 10.1109/TPDS.2018.2808959. url: https://doi.org/10.1109/TPDS.2018.2808959.

4.5 Machine Learning Approaches

[21]

Daniel D’Souza et al. “Graph Convolutional Network-based Scheduler for Distributing Computation in the Internet of Robotic Things”. The 2nd Student Design Competition on Networked Computing on the Edge. url=https://github.com/ANRGUSC/gcnschedule-turtlenet. 2022.

[35]

Habib Izadkhah. “Learning based genetic algorithm for task graph scheduling”. In: Applied Computational Intelligence and Soft Computing 2019 (2019).

[38]

Mehrdad Kiamari and Bhaskar Krishnamachari. “GCNScheduler: scheduling distributed computing applications using graph convolutional networks”. In: Proceedings of the 1st International Workshop on Graph Neural Networking, GNNet 2022, Rome, Italy, 9 December 2022. Ed. by Pere Barlet-Ros et al. ACM, 2022, pp. 13–17. doi: 10 . 1145 / 3565473 . 3569185. url: https://doi.org/10.1145/3565473.3569185.

[47]

Hongzi Mao et al. “Learning scheduling algorithms for data processing clusters”. In: Proceedings of the ACM special interest group on data communication. 2019, pp. 270–288.

[67]

Penghao Sun et al. “Deepweave: Accelerating job completion time with deep reinforcement learning-based coflow scheduling”. In: Proceedings of the Twenty-Ninth International Conference on International Joint Conferences on Artificial Intelligence. 2021, pp. 3314–3320.